△[はじめに]
今回は今までよりももう少し詳しくPE(したがってME)の分析を行い、数M的な考察を2つほど施してみた。
1つ目として、プランク長から示唆される3次元プランク体積について数M的考察を行う。これにより、この宇宙の構成についての理解を得ようと言うものである。
2つ目として、論理経路による相互作用のあり方について考察する。これまで漠然と「周りの論理」と結合する、などという曖昧な表現をより具体的に考察することを目指した。
これらにより数M理論は深掘りされ、より信憑性の高いものとして受け止められることを望む。
[目次]
★略号紹介
ME=数学的要素 PE=物理的要素
数M理論=数学的Mapping理論(本理論)
▲[プランク体積]
プランク長は物理的意味をもつ最小の長さであることはご存じであろう。したがってそこから容易に推察されるように現在の3次元宇宙空間はプランク体積即ち1辺1プランク長からなる立方体のようなもの(「向き」なる概念はない)の集合体として成立っていると考えられる。その中はそれ以上分解することはできず、単一の物理的要素が含まれているのみである。数M理論によればこの宇宙は数学の論理文のみからなり各PE=MEは完全一対一対応であることから今述べたプランク体積1つが1論理文であると仮定することは自然なことであろうし、また、後で述べるように私の理解の範囲内ではつじつまが合うのである。
ただ、まず一つ注意したいのはこの3次元プランク空間というのは現在の平衡状態の宇宙において我々がそれを認識する上で都合のよい概念と言うものであり、厳密なものではない。あくまで平衡状態の擬似空間なのである。
本にあるのは全順序全論理展開空間なのである。したがってこっちが変位している最中にあっちが・・・などといった事象が生じることはなく、整然と1プランク時間1論理展開が進行するのである。時空間により展開が歪むのではない。展開の結果時空が歪んでいる(ように見える)と言うだけである。
さて、このプランク空間のモデルは論理数が減ることのないモデルなのだとしたら現在の膨張宇宙の理由にもなる。実際、[論理経路]の部で述べるモデルでは論理数は減ることはないものとなっている。
また、論理の移動速度の限界が光速であると仮定すれば1プランク時間1プランク長の移動だからプランク空間の定義から1論理展開で各MEは「隣」のMEと作用、あるいはプランク空間へ移動することになる。
これはあくまでイメージとしての話なのだが、至って自然な物理モデルと言えると思われる。MEが隣のMEとしか作用しない、と言った事情が絡んでくるとはいえ、この議論の中で致命的な欠陥は見つからなかった。この「事情」に関して次の部で一定の答えが出る。
繰り返すが、このプランク体積の議論は現宇宙においての話であり、初期宇宙では初期論理展開があるのみで必ずしも3次元などと関わりがあるわけではなく、現宇宙の物理的意味が必ずしもあるわけではないことを注意しておく。
▲[論理経路]
では、論理経路についての話に議論を移そう。
ここで私の言いたいことは、これまで漠然と「周りのMEと相互作用する」と言う表現を多用してきたが、私はこの言い方に疑問符を抱くようになった。
と言うのも周りのPEとはあくまで「イメージ」であり、具体的にどのMEと作用してどのようなMEとは作用しないのかと言った規則に関しては全く言及していなかったからである。私は遅ればせながらこの点に気づいたのである。
仮にどのMEも全てのMEと作用するのだとしたら先の議論からそれは全て隣り合うプランク体積内に入っていなければならないということになり、この宇宙の存在を否定するという大惨事になってしまう。
また「同種の論理全て」と作用するのだとしても同様に同種の論理文が全て隣り合うから、同種のPE=MEが一カ所にのみ集中して存在することになり、現実世界と不適合である。
以上から何らかの関係があるME同士のみが反応すると考えられる。
そこで一つの「仮定」をし、それに従う「モデル」を考えた。
まずその「仮定」を述べると、「反応するのは同じ経路を辿ってきた(=過去の論理経路が一致する)論理のうち同型の論理だけである」と言うものである。
これにより、同種の論理のみ作用するのであり、かつその中の極一部であると制限できる。そしてそれらの論理が隣接すると考えるのだ。
次に「モデル」を考える。
そのモデルは最も簡単なものであり、1つの公理と1つの論理変位規則をもつものである。私の能力で解析可能なものと言う理由が大きく、この単純なモデルを選んだ。それでも私の解析が絶対に正しいと言いきる自信はない。
それでは紹介しよう。
公理: A
変形規則: 本の論理Lに対して過去に現れた任意の論理Kを選んでL∧Kが導出できる。また、どの論理とも結合せず、Lのまま導出することもできる。
[図]
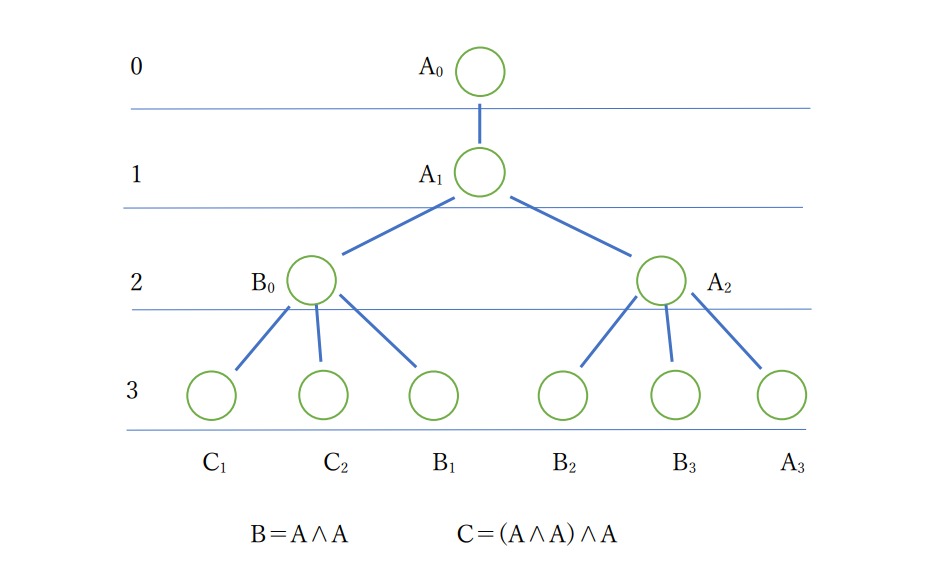
図を参照しながら読んでいただきたいのであるが、このように展開できることはお分かり頂けると思う。
ここで「仮定」の反応則を思い出していただきたい。
C1、C2は同型であり用いる過去の論理も同じ経路上のMEだから作用(反応)できる。これはまたB2、B3についても言える。ところがB1についてはB2、B3と同型でありながらも用いる論理はB0でありB2、B3の経路上にはない。したがってB1はB2、B3と反応しない。
直ぐ分かるようにこのモデルでは「仮定」の条件を満たす。
ちなみに第4段階を考えてみるとC∧B、C∧A、B∧B、C、B、Aの6種類の論理が導出される。これ以上の深入りをすることは避けておく。しかし、例えば
C∧B=((A∧A)∧A)∧(A∧A)
と言う形であり順序数に似たような形式をしていて興味深い。
以降読者の考察に任せることにしよう。(茶色:訂正)
また実際は公理の数や論理の導出規則も多かったり、複雑だったりすると思われる。しかし、私の知力では到底解析できないと思う。よってこれも考察は避けることにする。
最後につまらぬものだが今度はより具体的な式を用いた一例を挙げてみる。
参考までに。ここで上に出てきた記号「∧」は必ずしも「かつ」と読むものではなく、論理作用の「一種」として読むべきものであることに注意されたい。
[連立方程式]

代入法と加減法で論理経路が分裂する。(3)式と(4)式を合わせればx=-1,y=2なる答えに辿り着くがこれらは私のモデルでは直接には結べないのである。しかし、ともに原点を過去の論理としてもっているのでいずれも正解に辿り着く。付け加えると、(3)式と(4)式から誤った結論が導かれる例もある。
例
これでこれまで漠然と考えていた論理経路について一応の理解に至ったと考える。
△[おわりに]
本来、今回は英語版での執筆を行おうというつもりで書いてみたが、とても世界的な発表をするほどのレベルに達しないと思い至ったので、日本人向けの記事にすることにしたのである。
今回はまとめの作業をする中で考えがまとまらなくなってしまったため少々間が空いてしまった。その中で過去の記事を見返してみると第2号「MP等価性のおまけとして」で意外にもいいことを書いてあること気づいた。そこから考えが発展したことも多かった。
書きたいことはまだあり、今後も呟きができそうである。
それではまた!