数M[16]~数M創生からの発展~
[目次]
【はじめに】本稿では以前の記事の中でも特に重要な主張についての再確認を行います。散在していた重要な主張をまとめた形で再構成することを目指しました。
10年前、突如感じた違和感から始まり、衝撃的な結論へと至るさまをどうか共にお感じになっていただきたく執筆した次第であります。本稿では本理論の正当性は述べることはありませんが、その可能性について述べたつもりです。
正当性の主張については他記事
a)9号★~数M理論!~振り返ってみて思ったこと~ - 物理哲学!
b)12号★~数M理論![12]~相対性理論との融合~ - 物理哲学!
c)14号★~数M理論![14]~整合性の数々~ - 物理哲学!
などをご参照ください。
本理論が正しく、かつ哲学的内容から物理学的帰結への扉が開かれたなら、これ以上ない成果を生むことは間違いありません。万有引力や相対性理論の威力にも匹敵する可能性があると思っています。しかしその評価は読者の方々の考察にゆだねたいと思う次第であります。
尚、本稿は時系列で記載しました。少々回りくどくなっていますが、ご了承のほどよろしくお願いいたします。

まずは本記事の中で頻繫に使用される略号を載せておきます。
◆略号紹介
数M理論=数学的Mapping理論(本理論)
ME=数学的要素=Mathematical Element
PE=物理学的要素=Physical Element
本理論(数M理論)の発見は10年前の2014年に遡ります。私は大学時代から「物理学を追求することは数学を追求することに等しい」と漠然とながら思っていました。社会に出てから暫くそういったことを思い更けることはあまりなかったものの、2014年のあるとき大学の数学の教科書をペラペラめくるようなことをしていました。定理などを読んでいたのですが、ふとその時、そこに書いてある定理などが、物理学対象そのものなのではないか!?という考えが頭をよぎったのです。そのときです、背筋にゾクゾクとするような震えに近い感覚が走りました。この感覚は一体何だろう?と、頭をよぎったものを整理し、考え直してみようと試みました。ウィキペディアなどを多く参照していた記憶があるのですが、とにかく数学の各定理などが物理学対象そのもので一対一に対応しているのではないかという結論に落ち着いたのです。これを誰かに問うてみたいと今は消えてしまったある物理学掲示板に「質問」という形で投稿しました。その結果、以下の主だった2点の批判が返ってきました。
1.数理物理学と何か違いはあるのか?
2.数学的に意味のある定理などが必ずしも物理学的にも意味があるとは限らない。
これらの批判を受けた私は焦り、トンチンカンな答えをしてその場を去りました。気の小さい私からしたらかなりの冷や汗ものでした。これは発見から1年ほど経過した2015年のことだったと記憶しています。
(この当時から私の研究を「数M理論」という名で呼んでいました。)しかし、私はその研究活動をやめることはありませんでした。これらの批判が私の理論と相反するものではないと信じていたためでした。
さて、私はその後も研究活動を続けましたが、大した進展はなく研究活動も細々としたものになっていたと記憶しています。しかしある時です。論理学を知らなかった私は、論理学についての知識も得るべきだろうと論理学の本を読みました。なかなか読み進まない中、何とか読み終え、論理とは公理系を基軸に展開する論理式であるという認識に至りました。それと同時に「大事件」が勃発したのです。それは2017年のことでした。以下の2点について考察しました。
1.数学的要素=MEは論理展開と共に変位する。
2.物理学的要素=PEは時間と共に変位する。
さて、ここで数M理論の基本であるME-PE完全一対一対応を思い出して下さい。もしME=PEならばその変位の仕方もまた等価です。ところでMEの変位は明らかに(非稠密)可算型です(A→B→C→・・・)。従ってPEもまた同じ可算型となるはずです。よって時間には最小単位がある、と予想し調べて見たところ・・・あった!!そう、プランク時間なる時間の最小単位が!
このことから直ちに次の仮説が導出されます。
[仮説1]
MEとPEは完全に一対一に対応している。
最初に対応していたのはMEの原点とPEの原点である。即ち論理展開の始まりとビッグバンが対応していた。(論理展開は最初に設定されていた公理により規定される。)
論理展開と共にPEもまた発展してきた。
そのMP変位は1プランク時間毎に発生するであろう。
さて、どうでしょうか?この仮説が本数M理論の一つの到達点なのですが、どのように感じられましたでしょうか?ここにこの宇宙の真理が明瞭な形で言い切れています。ME-PE完全一対一対応の下、1論理展開というME空間の変位の最小単位が1プランク時間というPE空間の変位の最小単位に対応するという主張及び、ビッグバンの明確な定義が成されているのであります。そうなのです、ビッグバンとは他でもない論理展開の始まりのことだったのです!これこそが数M理論の最も重要な帰結であると言っても過言ではないと思います。
この宇宙の公理系が最初に設定されていて、そこから論理展開が厳然と1プランク時間に1展開ずつ実行されて行くのです。PE空間とはME空間の展開と共に発展するため初めの内は、その数は爆発的に増加し、ビッグバンのダイナミクス性を指し示していると考えられます。またこの論理体系が論理数の減らないモデルなのだとしたら現宇宙の膨張の理由にもなると考えられ、これは第9号★数M理論!~振り返ってみて思ったこと~ - 物理哲学!のツリーモデルで簡易的にみることができます。9号は一番評価の高い記事であります。
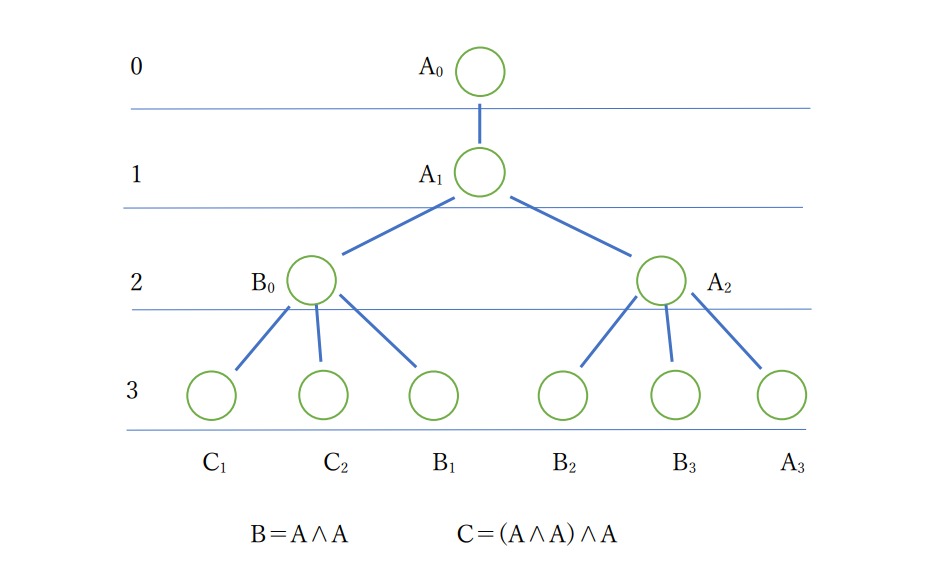
さて、我々もまたMEで、その論理展開の系内から周りのMEと作用し、それを認知しているのですが、それをあたかもMEとは別物のPEとして認識しているのです。しかしながら実際はPEとは我々がMEを認識した際の虚像であり、実質的には同一のものであります。言わば系内からみたPE=MEを考察するのが「物理学」であり、一方でMEを系外からそのまま認識するものが「数学」なのです。この系の内外という議題は第4号、6号、10号にも記載してあるので興味のある方はご参照願いたく思います。
上の[仮説1]が最初の数M的インスピレーションからビッグバンメカニズムの仮説導出までの流れでした。
一応、その後の流れも書き記したいと思います。
この劇的な結論を得た私はこれを正式な形で発表しようと、2018年暮れに科学雑誌Natureに投稿しました。ざっくりとした内容であったこともあり「そのような議論をする研究者にとっては確かに刺激を与えられるかもしれないが、確固とした論拠がないので出版の条件を満たさない」と一蹴されてしまいました。他の出版社にも投稿しようと考えましたが、暫く考えた結果、論文の域に達しないと判断し、次にKindle本の出版をしようと計画を変更したもののやはり考えが落ち着かず、その後もいろいろ画策しましたが結局手詰まりとなり、2022年1月にブログ第1号を発表しました。
その後ブログを書く中で時々考えが進むこともありました。例えば次の仮説導出のきっかけにもなりました。ただ、この仮説は似たような記述がブログ執筆前(2020年)の資料にも見られたため執筆前であった可能性もあります。
さて、次のような流れで仮説導出に至りました。
プランク長の定義から体積の最小単位なるプランク体積の存在を予想し、そして調べてみたところ・・・またもやあったのです!これはブログ執筆の前のことでした。
次の考察をしました。プランク体積が体積の最小単位であるからこの中には実体のある単一のPEのみが入っているでしょう。一方、実体のある単一のMEは1論理文であると考えられます。そして論理文の内容にはその文を特徴づける係数などの要素が考えられますし、文の展開の仕方として「解法」と言った要素も考え得ます。そしてこれら各種数学の対象はまたPEと一対一に対応しているのです。ここから次の仮説が導出されることになります。
[仮説2]
MEにおける各1論理文は各1プランク体積のPEと一対一に対応している。
更に推論を進めればこの1プランク体積内のPEに対し、そのPEを特徴づける温度・圧力などの状態量は対応する1ME文の係数値に対応する。
また、電磁場・重力などのPE間の作用素はME間の変位作用素、即ち「解法」に対応している。
この仮説のようにPEは体積をもつPE、状態量、作用素としてそれぞれ論理文、係数値、解法という種類のMEに対応していると考えられます。
[数M] ならば、解の比は―1:2である。
[通常] の2解の比を求める方程式は
である。
この例はここでの主張に対し、特に係数に関する通常研究と数M的研究法の対比であり、必ずしも良い例であると断言できるわけではありませんが、通常の方がより一般的な話をしているという点で、何となくの方向性は示せているような気がします。通常との差異の一例を、と思ったのですが少し脇道にそれてしまいました。
この[仮説2]は現宇宙の各種のPEとMEとの関係性を物語るものであり、中でも1プランク体積のPE=1論理文ということを主張することを強調しておきます。
さて、移動速度の最大値は光速であり、光速の定義から1プランク時間で1プランク長の移動速度となります。1プランク長隣には1PE=1論理文が存在することからこの光速移動は1論理展開毎、隣のMEと作用することを意味し、論理展開とこの「幾何」的宇宙空間との間に関係性をもたらすものであります。14号★数M理論![14]~整合性の数々~ - 物理哲学!に示した<1次元モデル>

をご参照ください。これは現宇宙空間を物語る上で至って自然な物理モデルであるとは思わないでしょうか?論理状態の安定した現在の3次元モデルでは1論理展開によって『隣』のPEと作用するのが通常であることになります。
もちろん隣のMEと作用せず停留することも考え得ます。この辺りのことは12号★数M理論![12]~相対性理論との融合~ - 物理哲学!などでも語ったことですが、この記事の絶対論理空間モデルは光速を考える際には完全に間違ったモデルであり、根本的に相対性理論と矛盾すると考えられます。これは以前の記事でも語ったことでもあります。ただ、光速を考えない通常の範囲では絶対論理空間も近似的には正しいような気がするのですが、どうなのでしょうか?読者の方々の考察にお任せしたいと思います。
以上、数M理論の創生、及びブログ執筆の中での発展の一部の確認をいたしました。他にも有益な考察が少々あると思いますので、ご興味のある方は過去の記事をご参照頂ければ幸いです。
さて、以後の予定としては英論記事をはてなブログで1本書いてから数M出版の執筆に取り掛かりたいと思っています。
それではまた!